What counts as knowledge

A theoretical and practical understanding of a subject?

What counts as knowledge?

Knowledge describes the theoretical and practical understanding of a subject. This definition is ambiguous if explored without examples.

This is a dictionary which translates Chinese into English. In John Seare’s famous Chinese room thought experiment, an English speaking man is alone in a room with a Chinese-English dictionary. He is fed instructions in Chinese, which he translates into English so he can execute them. To the instructor outside, the man in the room knows Chinese because he is understanding the Chinese instructions and executing them correctly. However, in reality, the man inside is all but translating the instructions into English and completing them. Regardless of ever learning Chinese, the man inside can communicate and follow instructions equivalent to anybody how can speak Chinese. Therefore, is it fair to suggest that the man inside has knowledge of Chinese when he is merely using the dictionary? An argument can be made that the man does not know Chinese because he is using a translating tool, only the dictionary knows Chinese. 

Therefore, taking this one step further, let’s assume the man inside has memorized, but not understood, the English-Chinese dictionary. He is capable of translating Chinese into English instantly, but cannot comprehend Chinese alone. Without the use of the tool, can it be said that the man inside knows Chinese? He can independently execute instructions and communicate with the instructor outside, like a native Chinese speaker. By definition, he does not know Chinese because he does not understand the subject itself. However, by practicality, he is able to perform all the tasks associated with the knowledge of Chinese. Externally, to the instructor or anybody outside the room, he has knowledge of Chinese, but internally he is just translating it from a memorized dictionary. 

However, simply memorising existing translation may limit the man inside. For example, consider a situation where a man is presented with a new Chinese phrase using the words in a manner that has not yet been specified by the current dictionary. Without an understanding of the structure of Chinese, the man may not be able to infer the meanings of new phrases as understood by Chinese speakers. Does this suggest that after all, the man does not know

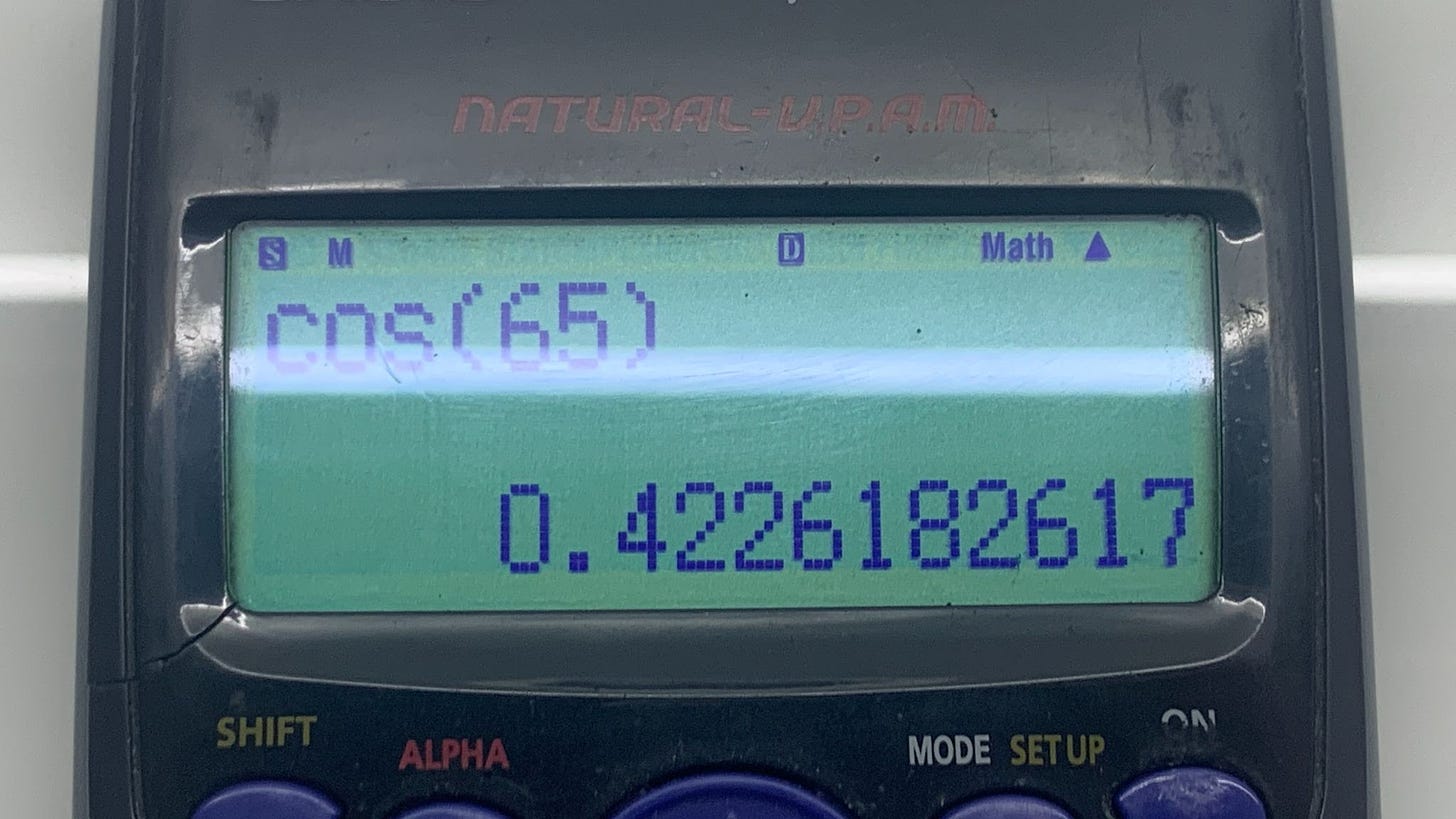
Cosine describes the trigonometric ratio of the side adjacent to an angle and the hypotenuse. This displays my calculator working out the cosine of 65 as approximately 0.42. As an HL maths student, my teachers will be disappointed to hear that I still rely on the calculator for the majority of my trigonometric values. Nevertheless, I understand how they are calculated and I have a calculator that can do it for me. Does that mean that I know what cos65 is? This is where the definition of knowledge conflicts with itself. Theoretically, I understand the foundation of cos65 but I am unable to practically perform my understanding without a computing tool, hence I am potentially dependent on my calculator knowing the answer. Nowhere is this more exemplary than on test day, at that dreaded moment when your calculator runs out of battery, you immediately ask for another calculator because the paper becomes impossible to solve otherwise. 

My classmates often bombard my maths teacher with questions like “why do I need to know this when I will have a calculator with me my entire life”. Essentially, what is the value of theoretical knowledge if it has no practical application, and more importantly, does the theoretical knowledge even count as knowledge if it is practically inapplicable in real life without secondary tools such as a calculator? I know what cos65 is theoretically as the trigonometric ratio of an angle with 65 degrees and I know that my calculator knows can work out cos65 given I press the correct buttons, but considering those two situations as mutually exclusive, my knowledge of cos65 as 0.42 becomes debatable and presents itself as a limitation of what really counts as knowledge.

This is the DVD of one of my favourite childhood television shows, the Flintstones. I would often sing their iconic theme song “Flintstones, its flinstones!” on repeat. Importantly, I would not pronounce the ‘T” in Flintstones and instead pronounce it as the Flinstones. It only recently came to my attention that the ‘T’ existed! Mysteriously, millions of other people have experienced the same realisation and have been mispronouncing it as well. This collective realisation has been dubbed as another manifestation of the Mandela Effect.

The Mandela effect is a phenomenon where a collective group of knowers experience a misunderstanding. It originates from when millions of people thought Nelson Mandela passed away in prison during the 1980s when in fact he died at age 95 relatively recently in 2013. This same phenomenon applies to the millions of people who mispronounced Flintstones as Flinstones, because the singer jumps over the ‘T’ very quickly, explaining why fans mispronounced it Flinstones, especially those at the age where they could not read yet.

I however still pronounce it Flinstones. Knowing this pronunciation is incorrect but transferring the same information, does it count as knowledge? We possess the same theoretical and practical understanding of how the show functions but communicated that understanding incorrectly, hence does it make that understanding incorrect? From my perspective, recognising that I have been mispronouncing the show counts as knowledge because I understand it is wrong. Does this affect the knowledge of the millions of viewers who still enjoy the show as Flinstones?

In conclusion, the definition of knowledge presents an abundance of limitations such as whether understanding depends on internal or external execution, the conflict between theoretical and practical knowledge and lastly the significance of correct and incorrect knowledge when communicating between knowers.

-V